webGL中在着色器中的二维有向距离场(SDF)及布尔运算的一些理解和使用

有向距离场

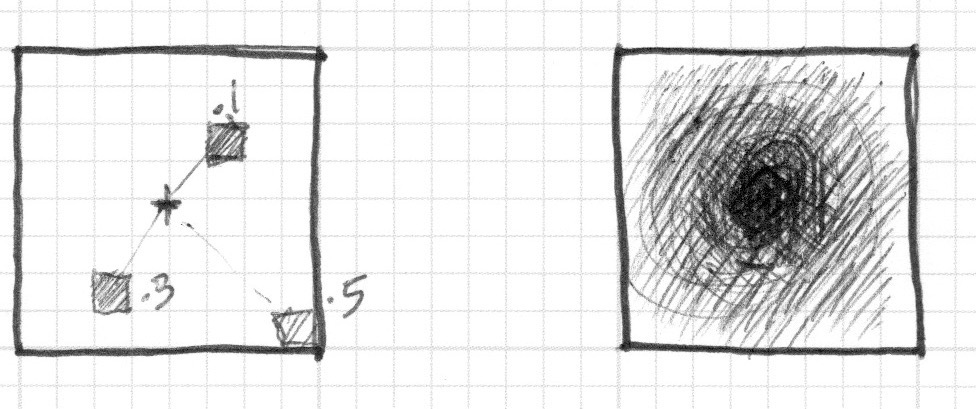
在着色器中绘图，类似于在一个方格纸上涂色，每个方格就是一个像素点。想象一下如果我们要在方格纸上绘制一个圆该怎么做呢，我们只需要把圆形内部区域涂成一个颜色，圆形外部区域的涂成另外一种颜色(或者不涂色)，这样我们便有了一个圆。在数学上我们怎么定义圆呢？及圆周上的点到圆心的距离等于半径，圆内部的点到圆心的距离小于半径，圆外部的点到圆心的距离大于半径。这样一圈一圈，我们可以在图上得到每一个点到圆心的距离，圆内部的点到圆心的距离减去半径为负值，圆外部点到圆心的距离减去半径为正值，因此我们称之为：有向距离场。

移动

在计算距离场的时候一般将坐标中点设置为原点，方便我们计算。但是通常，图形不是绘制在原点的位置，这样我们便需要原点位置设置在图形的中点，移动到原点是一个几乎所有图形都会用到的操作。如果图形的中点在(0.5,0.5)，那么将要将(0.5,0.5)设置为原点，我们只需要减去(0.5,0.5)，那么在绘制过程中便是以(0.5,0.5)为原点的。

vec2 translate(in vec2 p,in vec2 c) {
	return p-c;
}

圆形距离场

圆形的距离计算最为简单，我们只需要计算坐标到圆心的距离即可，假设圆心在(0.5,0.5)，由于着色器坐标归一化之后范围为[0,1]，那么绘图区域中点到圆心的距离范围为[0,0.5],如下图所示：

计算代码可以写为这样：

#ifdef GL_ES
precision mediump float;
#endif

uniform vec2 uResolution;

void main(){
  vec2 st=gl_FragCoord.xy/uResolution;
  vec2 center=vec2(.5);
  float dis=distance(center,st.xy);
  gl_FragColor.rgb=dis*vec3(1.);
  gl_FragColor.a=1.;
}

矩形距离场

矩形距离场稍微要复杂一些，假设矩形中点在正中心，长为w，宽为h，那么对于矩形内部的点来说，它们的x轴到中心的距离为[0,w/2]，它们的y轴到中心的距离为[0,h/2]；而矩形外面的的坐标，它们的x轴到中心的范围为[w/2,0]，它们Y轴到中心点范围为[h/2,1],如下图所示：那么减去长宽的一半之后，内部点x的范围为[-w/2,0]，外部点x轴范围为[-w/2+1,1],如下图所示：

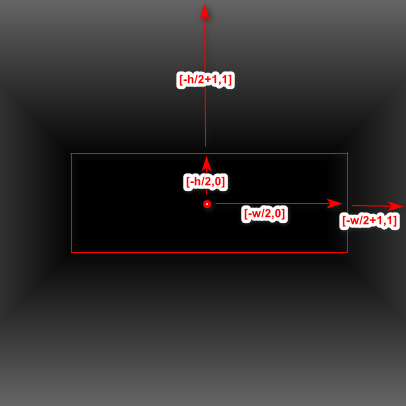
那么绘制矩形就有一个简单的方式了，矩形内部，x值和y值都必须小于0；矩形外部，x值和y值必然有一个是大于0 的，那么只要x，y的最大值小于0 ，就是矩形内部，否则，就是矩形外部，代码可以这样写

#ifdef GL_ES
precision mediump float;
#endif

uniform vec2 uResolution;

float plot_Rect(vec2 st,vec2 c,vec2 halfwh){
	// 移动到中心
	st-=c;
	// 以绝对值减去长宽
	st=abs(st)-halfwh;
	// 在矩形内部的点 x 范围为：[-w/2,0],同时 y的范围为[-h/2,0],所以，只要最大值小于0就可以表示点在矩形的范围
	return max(st.x,st.y);
}

void main(){
	vec2 st=gl_FragCoord.xy/uResolution;
	float dis = plot_Rect(st,vec2(0.5),vec2(0.3,0.1));
	gl_FragColor.rgb=step(dis,0.0)*vec3(1.0);
	gl_FragColor.a = 1.0;
}

对于更多更复杂的图形，绘制方法也是一样的，判断一个点处于图形内部还是图形外部就可以绘制他们，越复杂的图形，其距离场函数可能就会越复杂，需要有很深的数学功底，这些有一些距离场函数可以供参考：

shadertroy创始人的博客 (opens new window) 里面有许多2D乃至3D的距离场函数，可以通过这个图粗略的了解一下：

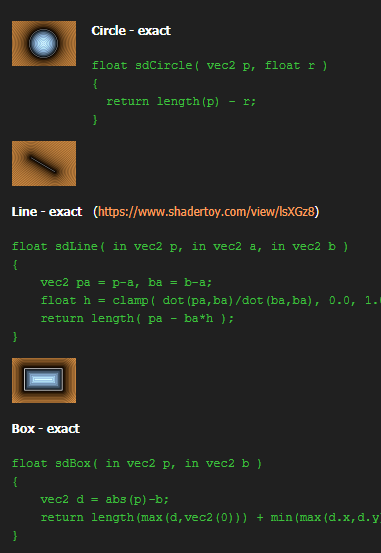
以及 the book of shaders大佬的vscode-glsl-canvas (opens new window) 这个插件里面包含了一些可用的2d sdf函数片段，可以参考.

还有国外一位大佬写的着色器教程 (opens new window)，很全面，很值得一看。

距离场布尔运算

通过距离场函数得到图形之后，可以通过布尔计算得到不同的组合，如下图所示，分别为圆于矩形进行交集（∩）、并集(∪)、差集(－)得到

代码如下图所示：

#ifdef GL_ES
precision mediump float;
#endif

uniform vec2 uResolution;

#include <lib/util.glsl>
#include <lib/shape.glsl>
#include <lib/color.glsl>

// 合并，取并集
float merge(float dis1,float dis2) {
	return min(dis1,dis2);
}

// 相交，取交集
float intersect(float dis1,float dis2){
	return max(dis1,dis2);
}

// 相减
float subtract(float base, float subtraction){
	return max(base,-subtraction);
}


void main(){
	vec2 st=gl_FragCoord.xy/uResolution;
	// 交集
	float c1 = sCircle(st,vec2(0.1,0.5),0.2);
	float r1 = sPoly(st,vec2(0.2,0.6),0.2,4);
	float dis1 = intersect(c1,r1);
	
	// 并
	float c2 = sCircle(st,vec2(0.5,0.5),0.1);
	float r2 = sPoly(st,vec2(0.5,0.6),0.1,4);
	float dis2 = merge(c2,r2);
	
	// 差
	float c3 = sCircle(st,vec2(0.8,0.5),0.1);
	float r3 = sPoly(st,vec2(0.8,0.6),0.1,4);
	float dis3 = subtract(c3,r3);
	
	float dis = merge(dis1,dis2);
	dis = merge(dis,dis3);

	gl_FragColor.rgb=fill(dis,AZUR);
	gl_FragColor.a=1.;
}

我们可以通过这些做出更有意思的图形，图形学的世界其实就是数学的世界，正如大师所说的，使用着色器绘图就如同将一艘船放进瓶子里，过程是如此的复杂，但是结果却很美丽。共勉！